パターン認識入門
3. ノイズ対策
カメラやスキャナで取り込んだ画像は、一般的には多くのノイズを含んでいます。人間の目では分からないのですが、判別分析法による閾値がこのノイズに大きく左右されて背景と文字を上手く区別できないことがしばしばです。
ここでは簡単なノイズ対策に触れておきます。
3.1 メディアンフィルターによるノイズ除去
ノイズを除去する簡単な方法は、メディアンフィルターを掛けることです。
メディアンフィルターとはある点とその周辺の全 9 点の明るさを調べ、その中で 5 番目の明るさをその点の明るさとする画像処理のことです。
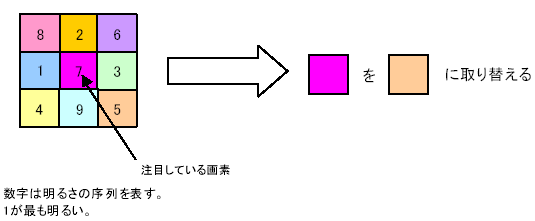
ここで 1 つ注意があります。それはこの変換では元の画像から新しい画像を作っていることです。決して 1 つの画像上で処理を行っているわけではありません。
このメディアンフィルターにより、パルスノイズをある程度除去可能です。
この処理結果の具体例は、次のようになります。


3.2 輪郭付近の画像に対して判別分析法を適用する
画像の中で意味を持つのはやはり輪郭です。多くの場合輪郭以外の部分は大した情報を含んでいません。無意味な部分に乗ったノイズの影響で有益な情報が取り出せなくなってしまっては困ります。そこで、先に挙げた判別分析法を適応する箇所を輪郭周辺に限定しましょう。
しかしここで新たな問題が発生します。どうやって輪郭を探すのか、という問題です。
輪郭を検出する手法にはいろいろありますが、今回はラプラスフィルターによって輪郭を検出することにしました。
説明の都合上ここでは画像を行列で表現することにします。行列 A に関してその ( i , j ) 成分を Aij と書きます。画像を行列で表現しますので、点 ( x , y ) の画素が持つ明るさが Ayx のように添え字が逆に書かれることに注意してください。但し座標に合わせるため、行の添え字も列の添え字も共に 0 から始めることにします。
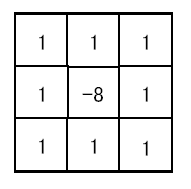
ラプラスフィルターもメディアンフィルターと同様に、注目している画素とその周辺あわせて 9 つの画素を見ます。
まず、次のような 3 × 3 行列 L を定義します。
図に描くとこんな感じです。
元となる画像を A、ラプラスフィルターにより得られる画像を B とすると、
という関係になります。得られた画像 B の画素の中で明るいものが輪郭を表します。
具体的には、次のようになります。

こうして得られた輪郭に対して先に説明した判別分析法を用いると、背景と文字を精度良く区別できます。
4. 輪郭線の検出
パターン認識に図形全体の情報を用いることもありますが、今回の文字認識アプリケーションでは対象となる文字の一番外側の輪郭線をなぞり、その形で文字を認識しています。この方法では輪郭線が 1 本の閉曲線になっていないと正しく認識できません。
3.2. でラプラスフィルターによる輪郭検出を説明しましたが、ラプラスフィルターで検出される輪郭は一般に幅を持っています。幅を持った輪郭線の幅をなくす処理も原理的には可能ですが、今回は簡単に、周囲にある文字を構成している点の数を画像中の各点について調べ、その数が 46 であるものを輪郭であると見なすようにしました。2. の 2 値化処理後の画像で言えば、値が 1 である全ての点についてその周囲 8 点にある値が 1 である点の個数を調べ、その数が 46 であれば、その点は輪郭であると判断するのです。
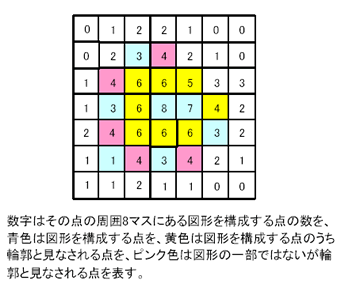
簡単ですね。
5. 複素 PARCOR(パーコル)係数法
輪郭も検出できたので、あとは図形の形を捉えることができればパターン認識が可能になります。今回はパターン認識に「複素 PARCOR 係数法」を用いました。
パターン認識の分野で複素 PARCOR 係数と言えば、ある図形についてその値を計算すると、その値がその図形を象徴する値となる値のことです。
この文字認識アプリケーションでは、あらかじめ見本となるアルファベットの大文字 A 〜 Z について複素 PARCOR 係数を計算して保存しておきます。そして、カメラで撮影した画像から PARCOR 係数を計算して、見本の文字の中から最も近い PARCOR 係数を持つものを選択することで、文字認識を行っています。
この辺りの理論については専門書に譲ることにして、ここでは複素 PARCOR 係数の計算方法について簡単に説明します。
まず 4. で検出された輪郭について、認識に使う点を決めましょう。全部使うことも出来ますが、その場合図形の拡大や縮小の影響を受けますので、今回は輪郭を反時計回りに 1 周しながら、等間隔に 128 個取り出すようにしました。以後説明のため、取り出す輪郭上の点の数を N 個としておきます。
次にその N 個の点について周回方向を決め、0 から N-1 まで順に番号付けします。j 番目の点の座標を ( xj , yj ) と表すことにします。ただしこの座標はこの図形の重心からの相対座標です。具体的には、画像上の実際の座標が ( x'j , y'j ) であるとき重心の座標 は
であり、
です。
各点を複素平面上の点と考えて、各点の座標を複素数 { zj } で表します。
そして、複素相関係数 を次のように定めます。
ここで " n mod m " は " n を m で割った余り " を表します。また、z* のように文字の上にアスタリスクがついたものは、その共役複素数を表します。
最後に、行列 A と複素 PARCOR 係数 を以下の規則で計算して行きます(行列の添え字は 1 から始まります)。
のとき
のとき
こうして得られた複素 PARCOR 係数 はその図形を拡大・縮小をしても、回転させても、平行移動しても変わりません。
あとは識別したい文字や図形について予め計算しておいた複素 PARCOR 係数と比較すれば、認識作業は完了です。











